오늘 Nature 紙에 구글의 quantum supremacy 달성에 대한 연구 논문이 게재되었고*,
*
https://www.nature.com/articles/s41586-019-1666-5
예상했다시피, 국내외, 관련 커뮤니티는 벌써부터 뜨겁게 달아 오르고 있습니다. 'quantum supremacy'라는 용어가 2019년의 연구 페이퍼에서 주장되기에는, 다소 이르고 과장된 개념이라는 이야기도 있고, 급속도로 발전하고 있는 딥러닝 등의 AI 기술과 맞물려, 인간이 컴퓨터와 로봇의 지배 하에 놓이게 될 날이 더 가까워졌다고 성급하게 절망하는 시각도 있습니다. 그렇지만, 어떤 스펙트럼의 시각이든, 논의를 더 단단하게 만들기 위해서는, 일단 이 'quantum supremacy'라는 개념을 정확하게 이해하는 것이 우선적으로 필요합니다.
Quantum supremacy (양자 우월성)는 'supremacy'라는 단어에서도 알 수 있듯, 양자 컴퓨터가 기존의 컴퓨터 (classical computer)의 성능을 압도하는 것을 의미합니다. 'Superemacy'라는 단어가 주는 '쿨함'의 폭만큼, 이에 대한 이해의 폭도 제각각인데, 사실, 오해의 소지는 바로 이 '성능의 압도' 라는 부분에서 시작한다고 볼 수 있습니다. 예를 들어, 2019년의 최신식 모바일 워크스테이션은 1999년 당시의 평균 수준의 슈퍼컴 성능을 뛰어넘는데, 그렇다면, 2019년의 모바일 워크스테이션은 1999년의 슈퍼컴에 비해 supremacy가 있는 것일까요? 그렇지는 않을 것입니다. 20년의 시간 간격도 시간 간격이지만, 단위 시간, 단위 에너지 당 가용한 계산 소스 (memory storage와 temporal data에 대한 random access, fidelity, 그리고 CPU 클럭 수)의 order가 다르기 때문입니다. 결국, 같은 알고리듬으로 같은 조건에서 정규화한 상태에서, 성능 차이가 나는지를 들여다 봐야 할 것입니다.
같은 환경에서 같은 계산 소스를 활용했을 때임에도 불구하고, 계산 성능의 차이가 압도적으로 난다면, 무언가 '우월'하다는 것을 간접적으로 보여 주는 것일 수도 있겠지만, 이것만으로는 여전히 '우월성' 이라는 개념을 확실하게 공정한 링 안으로 끌고 오기는 부족합니다. 예를 들어, permutation entropy (순열 엔트로피) 라는, 일종의 데이터 복잡도 (complexity) 지표를 계산하는 알고리즘을 생각해 보겠습니다. 필자가 아는 범위 내에서는 이 알고리즘에 세 가지 종류가 있는데, tabulated permutation order patterns 데이타가 미리 갖춰졌는지 여부에 따라, 세 알고리즘의 계산 시간은 같은 계산 환경에서도 최대 100배까지나 차이가 납니다 (이 숫자를 잘 기억해 둡시다). 물론 바보가 아닌 이상, 같은 값이면 다홍치마라고, 잘 정렬된 table data가 지원되는 효율적인 알고리즘을 쓰는 것이 여러모로 훨씬 좋은 것을 알기 때문에, 그것을 쓰게 될 것입니. 그럼에도 불구하고, 이 알고리즘이 다른 느린 두 알고리즘에 비해 'supremacy'가 있는가? 라는 질문에는 'yes!'라고 단언하기가 어딘가 찜찜할 것입니다.
결국, 계산에 있어 supremacy라는 개념을 가지고 오려면, 단순히 계산 성능의 압도적 향상은 물론 (이는 충분 조건에 불과하다..), 전혀 다른 novelty가 필요 조건으로 양립되어야 합니다. 그것은 바로, 기존의 classical computer로 구동될 수 있는 알고리즘을 활용하여 '절대 풀리지 않던 문제 (불가능성)'를 양자 컴퓨터로 풀 수 있는 것을 보여야 하는 것입니다. 이번에 구글이 주도한 연구 결과가 실린 네이처 페이퍼의 저자들은 이른바 '양자 우월성'을 달성했다고 주장하면서, 이에 대한 근거로서, classical computer로 무려 '만 년'이나 걸리는 문제 (i.e., pseudo-random quantum circuit problem**)
**
https://doi.org/10.4230/LIPIcs.CCC.2017.22
를 겨우 '200초'만에 풀었다는 벤치마킹 데이터를 제시하였습니다. 이 데이터를 통해, 그들이 개발한 양자 컴퓨터가 최초로 'quantum supremacy'를 달성했다고 주장한 것이죠. 물론 이것을 액면 그대로 받아들이는 사람들도 있겠지만, 앞서 언급한 '불가능성'의 기준으로 봤을 때는, 구글의 컴퓨터가 quantum supremacy를 달성한 것이 아니라는 주장도 있습니다. 이 중, 가장 대표적인 시각은, 이 논문이 출판되기 이틀 전에 발표된 IBM의 입장문이라고 생각합니다. 아마도, 9월에 잠깐 NASA 홈피에 유출된 preprint 버전의 페이퍼에 대한 코멘트로 보이는데, preprint 버전과 오늘 네이처에 공개된 버전이 큰 차이가 없으므로, IBM의 입장에는 변화가 없을 것이라 가정하겠습니다. 양자 컴퓨터 개발에 있어 구글의 가장 강력한 경쟁자이기도 한 IBM의 입장은 (경쟁자로서의 질시나 우려가 아닌) 객관적 비교 데이터에 의거한 objection이라고 할 수 있습니다.
IBM은 그들의 최신 알고리즘에 근거하여, 기존의 classical computer로도 구글이 언급한 동일한 문제를
"We argue that an ideal simulation of the same task can be performed on a classical system in 2.5 days and with far greater fidelity. This is in fact a conservative, worst-case estimate, and we expect that with additional refinements the classical cost of the simulation can be further reduced."라고 주장했는데, 즉, '최악의 경우라도' 2.5 일만에 해결할 수 있음을 주장한 것이죠 (그럴만한 충분한 결과를 IBM은 이미 지난 몇 년 간 circuit partitioning, tensor contraction deferral, gate aggregation and batching, careful orchestration of collective communication, and well-known optimization methods such as cache-blocking and double-buffering, optimization of hybridization of the CPU and GPU components on the hybrid nodes 등, 각종 알고리즘으로 증명한 바 있습니다.).***
***
https://www.ibm.com/…/resear…/2019/10/on-quantum-supremacy/…
아마도, IBM의 주장에 따른다면, 모든 조건이 잘 튜닝되고 최적의 알고리즘을 활용한다면, '수 시간' 이하로 동일한 문제에 대한 계산이 끝날 가능성이 높다고 보는 것인데, 이렇게 된다면, 벤치마칭은 구글의 주장대로 200 s vs 10^4 yrs (~3*10^11 s)로 벌어지는 것이 아닌, 200 s vs 20,000 s 정도로 엄청나게 좁혀지게 됩니다. 즉, 구글의 비교는 무려 10^9 배의 차이인데, IBM의 비교는 100배, 즉, 10^2 밖에 안 되는 차이인 것이죠. 두 그룹 사이에는, 10^7이라는 거대한 격차가 있는 것입니다. 마치, '나무늘보 vs. 로켓'의 대결 같은 뉘앙스가, '나무늘보 vs. 거북이' 대결 정도의 뉘앙스로 tone-down되는 것이라고 할 수 있겠습니다. 이 정도 수준이라면, 앞서 순열 엔트로피 계산의 사례에서 언급된 정도 (즉, 100배 정도의 계산 속도 차이)로 볼 수 있는 것인데, 달리 말하자면, 그냥 성능 좋은 알고리즘을 '잘' 쓴 결과에 불과하므로, 진정한 'quantum supremacy'라고 칭하기 어렵다는 쪽에 무게가 실린다고 보는 것이 합리적일 것 같습니다.
그럼에도 불구하고, 오늘 공개된 구글의 양자 컴퓨터는, 어쨌든 50개 이상의 qbit의 결맞음 (quantum coherence) 시간을, 어쨌든 전인미답의 수준인 '수백 초' 단위로 0.2% 수준의 오류율을 넘기지 않으면서, 제어할 수 있음을 실험적으로 증명한 것이기 때문에, 그 자체로 대단한 기술적 혁신이고, 엄청난 과학적 진보임에는 분명합니다. 결국 관건은, 이렇게 혁신적인 계산 성능을 갖춘 양자 컴퓨터가 과연 기존의 classical computer로는 해결할 수 없는 문제를 푸는데 성공할지 여부일 것입니다.
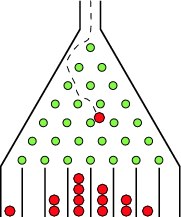
사실 이 문제는 컴퓨터 과학에서도 그렇지만 수학에서도 굉장히 중요한 문제입니다. 결국, classical computer, 그리고 classical computer에서 '어쨌든 이론적으로라도' 구동될 수 있는 모든 알고리즘을 동원하여 풀리는 문제는 '다항시간 (polynomial time)' 동안에 풀리는 문제일 것이기 때문에, 만약, 다항시간 동안 풀릴 수 없는 문제가 있고, 그것을 양자 컴퓨터가 풀 수 있다면, 그것이야 말로, 양자 컴퓨터의 'quantum supremacy'를 빼도박도 못하게 증명하는 것이 될 것이기 때문입니다. 이에 걸맞는 문제로 앞서 언급한 'pseudo-random quantum circuit problem' 같은 문제보다는, 무언가 더 근본적으로 계산이 매우 어려운 문제가 필요합니다. 그 문제의 대표 케이스가 바로 보손 샘플링 (Boson sampling)이죠. 이 문제를 쉽게 이해하기 위해서, Galton board (첨부 그림 참조) 같은 애들용 장난감을 유비로 활용할 수 있습니다. 이 장치의 입구에 공을 하나씩 떨어뜨리면, 공은 얆은 수직 기둥 여러 개에 순차적으로 이리저리 부딪히다가, 바닥에 놓인 여러 개의 bin 중 어느 하나의 bin으로 떨어지게 된데. 이제 공을 수십 수백 개를 차례로 떨어뜨리면, 이들이 어느 기둥에 어떻게 (즉, 어떤 각도와 모멘텀으로) 부딪힐 것인지는 기둥의 개수와 간격 등에 의해 조절될 것이고, 많은 공을 떨어뜨릴수록, 중앙에 가장 많이 모이고, 양 끝으로 갈수록 가장 적게 모이는 정규 분포 (Gaussian 분포) 같은 모양새를 갖게 될 것입니다.
이러한 galton board는 내부의 기둥의 개수가 많을수록, 그리고 기둥의 특성을 제어할수록 더 정교한 분류 작업을 시행할 수 있게 됩니다. 그렇지만, 이 실험을 컴퓨터에서 하기는 결코 쉬운 일이 아닙니다. 공이 어떤 bin에 떨어지게 될지의 확률 분포 계산은 내부의 기둥의 개수 (N이라고 하자)를 차원으로 갖는 행렬의 복잡도에 의해 결정되기 때문이죠. 특히, 이 공의 착륙 확률 분포는 N*N 행렬의 permanent라고 하는 행렬 특성의 절대값에 비례하는 양상을 보이는데, 사실 행렬의 permanent 계산은 classical computer로 계산하기가 '매우매우매우' 어려운 문제에 속합니다.
(정방) 행렬 (square matrix)의 permanent는 행렬식과 일견 매우 닮았습니다. 정방 행렬의 행렬식 (determinant)은, 잘 알려져 있다시피, 행과 열이 독립된 성분끼리, 순서를 따져가며 부호를 결정하여 곱한 값들의 합이다. 예를 들어 A =
[a b; c d] 같은 2*2 행렬의 행렬식은 det(A) = (a*d - b*c) 입니다. 그런데, 이 행렬의 permanent, 즉, perm(A)는 perm(A) = (a*d + b*c) 이죠. 행렬식과 닮았지만, 부호가 모두 +로 통일된 것을 볼 수 있습니다. 부호가 행과 열의 순서에 의존하는지 여부가 이것만 봐서는 큰 영향이 없는 것처럼 보일 수 있지만, 행렬의 사이즈가 커질수록, 이 차이는 어마어마한 차이로 발전하게 됩니다. 같은 사이즈의 행렬이라고 해도, 사실, 행렬식의 계산은 '비교적' 쉬운 편입니다 (사실, 이는 인류에게 있어 현대 문명을 일으키는 과정에서 만난 대단히 큰 행운이기도 하죠. 전자 (electron)이 페르미온이 아닌 보손이었다면, 양자역학이 전자공학으로 연결될 수 없었을...). 즉, 선형대수를 들은 학부생들이라면 치가 떨리도록 연습해 봤을 가우스 소거법부터, LU decomposition 같은 방법을 활용하면, 행렬식 계산은 classical computer로 다항 시간 (polynomial time)동안에 계산되는 것이죠. 보통 O(N^2)에서 최악의 경우라도, O(N^3) 스케일의 시간이면 계산이 가능합니다. 즉, 행렬식 계산은, 행렬의 크기가 아무리 크더라도, 어쨌든 이론적으로 계산 가능한 P-class 문제라고 할 수 있습니다. 그런데, 그 사촌 격인 perm(A) 계산은 그렇지 않다는 것이 critical한 문제가 되는 것입니다.
가장 간단한 케이스인 정방 이진 행렬 (square binary matrix)의 경우 (즉, 행렬의 모든 성분이 0과 1로 이루어진 정방 행렬)의 경우에도, 이 행렬의 perm(A) 계산은 NP-hard 문제로 알려져 있으며, 이 말인즉슨, 결국 지금까지 알려져 있는 classical computer와 알고리즘으로는 perm(A)의 다항시간 이내의 계산이 '불가능'하다는 것을 의미합니다. 반대로, 만약, 양자 컴퓨터와 양자 컴퓨터에서만 돌아가는 알고리즘을 활용하여, perm(A)의 계산을 다항 시간 이내로 할 수 있다면, perm(A)의 문제는 더 이상 NP-hard 문제가 아니게 되고, 이는 'P = NP' 문제****
****
https://en.wikipedia.org/wiki/P_versus_NP_problem
에 대한 매우매우매우 중요한 실마리를 제공하게 될 것입니다. 사실 이 부분 때문에, 일부 수학자들과 컴퓨터 과학자들은 양자 컴퓨터를 P vs NP 문제의 데우스 엑스 마키나로 기대하는 사람들도 있긴 합니다.
Galton board에서의 perm(A) 계산을 훨씬 작은 스케일, 즉, 나노 스케일에서 거의 그대로 재현할 수도 있습니다. 그것이 바로 quantum linear inteferometer입니다. Galton board의 기둥 대신, linear interferometer를 일정한 간격으로 배치하고, 이들을 galton board처럼 다이아몬드 혹은 삼각형 격자로 배열한 후, 쇠구슬 대신, 광자 (photon) '한 개'를 이 간섭계 네트워크에 쏩니다. 그러면, 광자는 간섭계 네트워크를 거치며, 고유 모드가 결정되고, 1~M 까지 이론적으로 가능한 모드 중, 특정한 모드를 갖게 될 것인데, 그 특정한 모드를 갖게 될 확률은, 간섭계 네트워크를 수학적으로 표현한 행렬 (보통, unitary matrix)의 perm(A)에 비례합니다. 여기서 중요한 것은, 광자가 보손 (boson)이라는 사실입니다. 기실, galton board의 쇠구슬도 서로 독립이고, 대칭성을 가지므로, 일종의 'effective 보손'이 되고, 그래서 행렬의 perm(A)가 확률 분포의 주요 factor로 활용된 것임을 고려하면, quantum linear interferometer network의 광자 분류기에서 광자가 보손이기 때문에, perm(A)가 이들의 확률 분포 인자로 활용되는 것은 당연한 이치로 보입니다. 왜냐하면 보손은 symmetric하고, 따라서 행과 열의 순서 조합을 구분하기 위한 부호가 의미 부여 안 되기 때문입니다. 참고로, 광자 같은 보손이 아닌, 전자 같은 페르미온 (fermion)을 활용했다면, 페르미온은 anti-symmetric이기 때문에, 행렬 성분 조합의 순서에 부호가 의미 부여되고, 따라서 확률 분포는 perm(A)에 비례하는 것이 아닌, det(A)에 비례하게 될 것입니다.
2012년, Aaronson과 Hance는 quantum optics 시스템을 가정하여, perm(A) 계산을 직접적으로 할 수는 없지만, bin에 쌓인, 즉, 특정한 mode를 갖는 광자의 확률 분포를 계산함으로써, 역추정, 즉, 샘플링이 가능함을 보였습니다.*****
*****
https://eccc.weizmann.ac.il/report/2012/170/
물론 이론적으로만 추정한 것이었지만, 어쨌든 가능하다는 것을 보였기 때문에, 이제 관건은, reliable한 single photon source를 찾는 것과, 광자 한 개와의 interaction potential이 거의 fix된 linear interferometer를 실험적으로 구현하는 것 (그것도 굉장히 작은 스케일 (수 nm)에서) 이 될 것입니다. 앞서 언급한 것처럼, 광자는 보손이기 때문에, 이 방법을 보손 샘플링 (boson sampling)이라고 합니다. single photon을 하나씩 쏘는 방법도 있지만, 어짜피 광자는 모두 동일하므로, 여러 개의 광자를 동시에 쏘는 방법도 있는데, 이 방법은 근사적 보손 샘플링 (approximate boson sampling)으로 불립니다. 사실상 Exact boson sampling은 hard NP 문제에 가까우므로, exact boson sampling algorithm을 찾는 것은, 자물쇠를 여는 열쇠를 얻기 위해, 다른 자물쇠의 열쇠를 찾는 것과 비슷한 이치라, 이를 우회할 수 있는 방법이 필요한 것이고, 그나마 실험적으로 시도할 수 있는 방법이 바로 approximate boson sampling인 것이죠. 물론, 'approximate'이기 때문에, 여기서 얻어진 실험적 확률 분포 (mode distribution)이 얼마나 정확하게 perm(A)를 추정할 수 있는지는 한계가 있으며, 오차를 줄이는 핵심은, 같은 성질을 가지고 있는 독립적인 보손을 얼마나 동시에 많이 쏠 수 있느냐에 달려 있다고 할 수 있습니다. 이를 quantum optics에서 구현한 것이, quantum linear interferometer network 인데, 보손으로서의 광자를 사용하고, 간섭계의 크기와 간격, 유전률을 초미세 패터닝으로 구현하고 외부 전기 신호 등으로 제어함으로써, approximate boson sampling을 가능하게 할 수 있습니다. 문제는, 동시에 쏠 수 있는 보손, 즉, 광자의 개수에 제한이 있을 뿐더러, 20개 이상의 보손의 확률 분포 계산은 기존의 classical computer로는 추적이 불가능하다는 것입니다.
양자 컴퓨터가 담당할 부분이 바로 여기 있습니다. 기존의 classical computer로는 접근이나 추정이 불가능한 multi-boson sampling이 가능하게끔 만드는 것이죠. 당연히 이를 위해서는, 앞서 언급한 quantum optics 실험 셋이 구현되어야 할 뿐더러, 기존의 classical computer에서 작동되는 알고리즘이 아닌, 양자 컴퓨터 전용 알고리즘, 즉, 보손의 중첩을 고려하는 알고리즘이 필요합니다. 그리고, 이 알고리즘으로, (approximate) boson sampling 문제가 다항 시간 스케일 수준으로 풀릴 수 있음을 보여야 할 것입니다. 이렇게 된다면, 비로소 양자 컴퓨터가 classical computer에 비해 'quantum supremacy'를 보였다라고 주장할 수 있을 것입니다.
오늘 네이처 지에 출판된 연구 내용 이상으로, 제 개인적 느낌적 느낌으로는, 구글 내부의 양자 컴퓨터 연구팀은 아마도 더 막강한 하드웨어와 더 막강한 알고리즘을 감추고 있을 가능성이 있다고 생각합니다. 아마 일부는 영원히 대중에게 공개되지 않을 것 같습니다. 그리고, 그 가운데, 바로 이 approximate boson sampling이 가능하게 되는 알고리즘과 꽤 fidelity가 높은 시스템도 이미 구현되었을 (혹은 생각보다 이른 미래에 구현될) 가능성이 높다고 봅니다. 이에 대해 과연 IBM이 먼저 장군을 부르며 응수를 내어 놓을 것인지, 아니면 구글의 다음 수를 더 기다릴 것인지 지켜 보는 것도, 이 분야에 조금 발을 걸치고 있는 연구자의 입장에서는, 매우 흥미로운 부분이기도 합니다.
한 가지 다시 한 번 유념할 부분을 이야기하고 이 글을 매조지하는 것이 좋을 것 같습니다. 설령, 언젠가 양자 컴퓨터가 boson sampling 문제를 다항 시간 이내로 풀 수 있는 시스템을 갖추게 되더라도, 이른바, P = NP 문제가 확고하게 증명되는 것은 아니며, RSA를 비롯하여 세상의 모든 암호가 당장 무력화되는 것도 아니고, 스카이넷이 인류 위에 군림하게 되는 것은 더더욱 아니라는 것입니다. 그저, 심해에 도달하거나, 화성에 유인 우주선이 착륙하거나, 무인 우주선이 성간 우주에 진입하게 되는 것처럼, 인류가 아직 역사 상 한 번도 디디지 못한 영역에 발자국 하나를 더 깊게 남길 수 있다는 것, 그 이상도 그 이하도 아닐 것이라고 생각합니다.
다만, 막강한 자금과 인력과 시스템이 갖춰진 구글이 evil이 되지 않기만을 바랄뿐이죠.