|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
20/03/20 21:20
(수정됨) 답변 감사합니다.
말씀해주신대로 생각해보니깐 직관적으로 최단거리가 그려지는데 접힌 직사각형이라는게 사각형 윗변에 대칭되는 가상의 사각형을 그리고 좌측하단 모서리부터 우측상단 모서리까찌 직선을 그리는걸 상상했는데 그러면 직사각형이든 정사각형이든 모든 경우 사각형 윗변의 정중앙을 찍고 갔을때가 최단거리가 되는게 맞을까요? 제가 이해를 제대로 했는지 모르겠는데 맞다면 질문4번 5번에 대한 궁금증이 풀렸네요. 감사합니다.
20/03/20 22:13
질1) 원에서 각도 theta에 따른 점 a와 점 b 사이의 거리를 합한 다음 theta에 대해서 미분해서 0이 나오는 각도를 찾은 뒤 조사하면 될 것 같습니다. 더 쉬운 방법이 있을 것 같긴 한데, 떠오르지는 않네요.
질2) 직관적으로 생각했을 때 (대체적으로) 접점이 d에서 e로 이동하는 중에 길이가 줄어들었다가 다시 늘어날 것으로 생각합니다. 질3) 상황에 따라 답이 달라집니다. 질4) 위에 답이 있습니다. 질5) 최단거리 위치는 중앙이고, 가로 길이가 달라지면 (좌표값이) 변동이 될겁니다.
20/03/20 22:33
제가 배움이 짧아서 질문1에 대한 답변이 이해가되질 않네요..ㅜㅜ 7차과정이라 미분은 배우질 않았는데 혹시 더 쉽게 설명해주실 수 있을까요ㅠㅠ
그리고 질5에 대한 답변은 좌표값이 변동된다는게 어떤 의미일까요? 항상 중앙을 찍고 가는게 최단거리가 아니라는 말씀이신가요? 질4에 답이 있다고 하는데 제가 정확히 이해를 한게 맞는지 모르겠습니다..
20/03/20 22:39
많은 최단거리 구하기 문제의 솔루션으로 미분이 제시되기 때문에 이 부분은 미분 없이는 풀기 어렵지 않나 싶습니다;
대략적으로 말씀드리면, 좌표를 아주 조금씩 옮겨가면서 경로의 길이가 늘어나는지, 또는 줄어드는지 그 정도를 보는 것이 미분입니다. 아마 점을 옮겨갈수록 길이가 점점 줄어들다가, 어느 순간엔 더이상 줄어들지 않고 바로 다음 순간에는 경로 길이가 다시 늘어나게 될텐데, 이 때 경로가 줄어들지도, 늘어나지도 않는 (미분했을때 0이 나오는) 지점이 최단거리가 된다는 식입니다. 5번은 위에서 이해하신 내용이 맞습니다.
20/03/20 22:52
넵 친절한 답변감사드립니다.
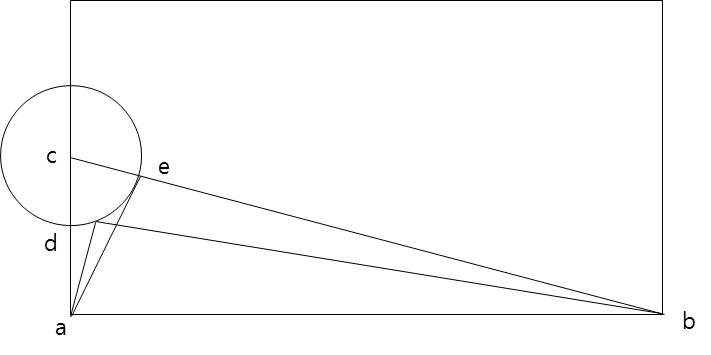
마지막으로 질문드리면 최단거리는 d와e사이의 접점에 있고 그위치는 사각형 가로의길이와 원의크기에 따라 달라질거라고 말씀하신게 맞나요? 제가 본문에는 못적었는데 직관적으로 느낄때 원의 크기와 사각형 가로의 길이의 변화와 관계없이 항상 d가 최단거리일거 같은데 이건 틀린생각이겠죠?(근거는 없습니다만...)
20/03/20 23:06
네, 이해하신대로 (일부 특수한 경우를 제외하고) 일반적으로는 최단거리가 d와 e 사이의 점을 통과하는 게 맞을거고, 그 위치는 상황에 따라 달라집니다.
가령 가로가 6, 세로가 3인 박스를 그리고 점 a의 위치는 (0,3) 점 b의 위치는 (6,3) 이라고 하고, 점 c의 위치는 (0,1), 그리고 점 c를 중심으로 하는 원의 반지름이 1이라고 했을 때 점 d의 위치는 (0,2)가 될 거고... 이 때 원 위의 점 x를 놓고 선분 ax + 선분 bx 의 길이가 최단이 되는 각도 dcx 는 0도가 아니라 대강 56도 근처쯤이 됩니다. 위 예시는 계산이 귀찮아서 그냥 엑셀에 여러 각도 때려넣고 값만 구해본 것임을 일단 밝힙니다...
|
||||||||||||||